Contains Duplicate

LeetCode Question 217 Medium

Krishna Shrivastava

January 10, 2026

14 views

LeetCode Easy HashMap

LeetCode Problem 217

Link of the Problem to try -: Link

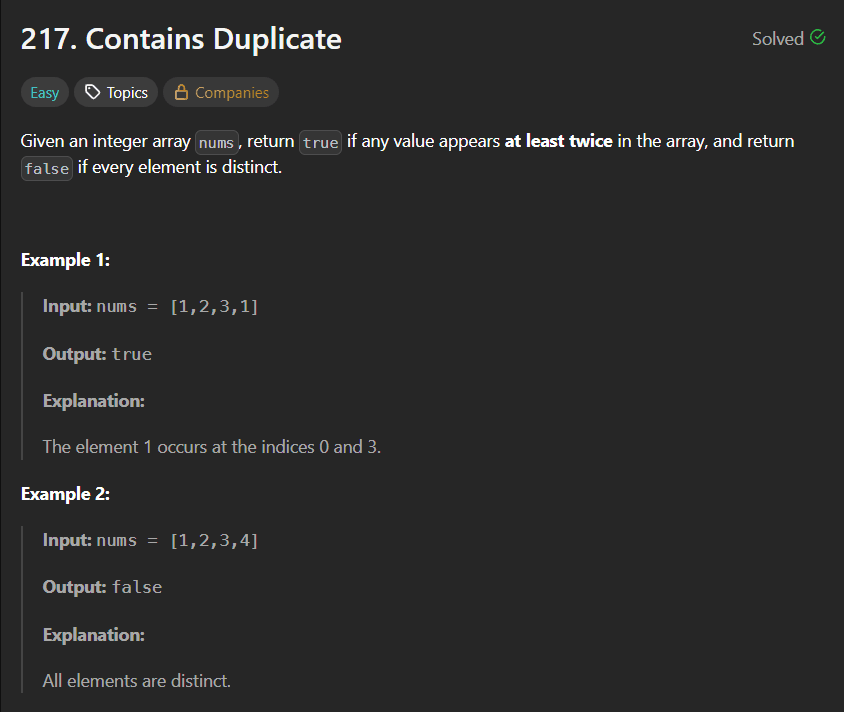
Given an integer array nums, return true if any value appears at least twice in the array, and return false if every element is distinct.

Example 1:

Input: nums = [1,2,3,1]

Output: true

Explanation:

The element 1 occurs at the indices 0 and 3.

Example 2:

Input: nums = [1,2,3,4]

Output: false

Explanation:

All elements are distinct.

Example 3:

Input: nums = [1,1,1,3,3,4,3,2,4,2]

Output: true

Constraints:

1 <= nums.length <= 10⁵
-10⁹ <= nums[i] <= 10⁹

Solution:

1. The HashMap Approach

Using a HashMap is a highly effective way to track occurrences. Although we are only checking for the existence of a value, the HashMap logic allows us to store the element as a "Key" and its frequency as a "Value."

Logic:

Iterate through the nums array.
Before inserting an element, check if the HashMap already contains that key.
If it exists, you've found your duplicate—return true.
Otherwise, put the value into the map and continue.

Code:

public boolean containsDuplicate(int[] nums) {

HashMap<Integer, Integer> map = new HashMap<>();

for (int i = 0; i < nums.length; i++) {

// Check if the current number is already a key in our map

if (map.containsKey(nums[i])) {

return true;

}

// Map the number to its count (1)

map.put(nums[i], 1);

}

return false;

}

2. The HashSet Approach (Optimized for Storage)

While similar to the HashMap, the HashSet is often more appropriate for this specific problem because we only care if a number exists, not how many times it appears or what its index is.

Logic:

We initialize an empty HashSet.
As we loop through the array, we check ms.contains(nums[i]).
If the set already has the number, it's a duplicate.
This approach is preferred over HashMap for this problem because it uses less memory and has cleaner syntax.

Code:

public boolean containsDuplicate(int[] nums) {

HashSet<Integer> ms = new HashSet<>();

for (int i = 0; i < nums.length; i++) {

if (ms.contains(nums[i])) {

return true;

}

ms.add(nums[i]);

}

return false;

}

3. The Sorting & Two-Pointer Approach

If you want to avoid using extra memory (like a Set or Map), you can use the Two-Pointer method combined with Sorting.

Logic:

First, we sort the array. This ensures that any duplicate values are placed next to each other.
We use two pointers: j (the previous element) and i (the current element).
By moving these pointers across the array, we compare the values. If nums[i] == nums[j], a duplicate exists.

Code:

public boolean containsDuplicate(int[] nums) {

// Step 1: Sort the array

Arrays.sort(nums);

// Step 2: Use two pointers to compare adjacent elements

int j = 0;

for (int i = 1; i < nums.length; i++) {

if (nums[i] == nums[j]) {

return true; // Duplicate found

}

j++; // Move the previous pointer forward

}

return false;

}

Performance Summary

Approach	Time Complexity	Space Complexity	Recommendation
HashSet	O(n)	O(n)	Best Overall – Fastest performance.
HashMap	O(n)	O(n)	Good, but HashSet is cleaner for this use case.
Two Pointer	O(n \log n)	O(1)	Best for Memory – Use if space is limited.

Final Thoughts

Choosing the right approach depends on whether you want to prioritize speed (HashSet) or memory efficiency (Two-Pointer). For most coding interviews, the HashSet solution is the "Gold Standard" due to its linear time complexity.