GeeksforGeeks Problem
Link of the Problem to try -: Link
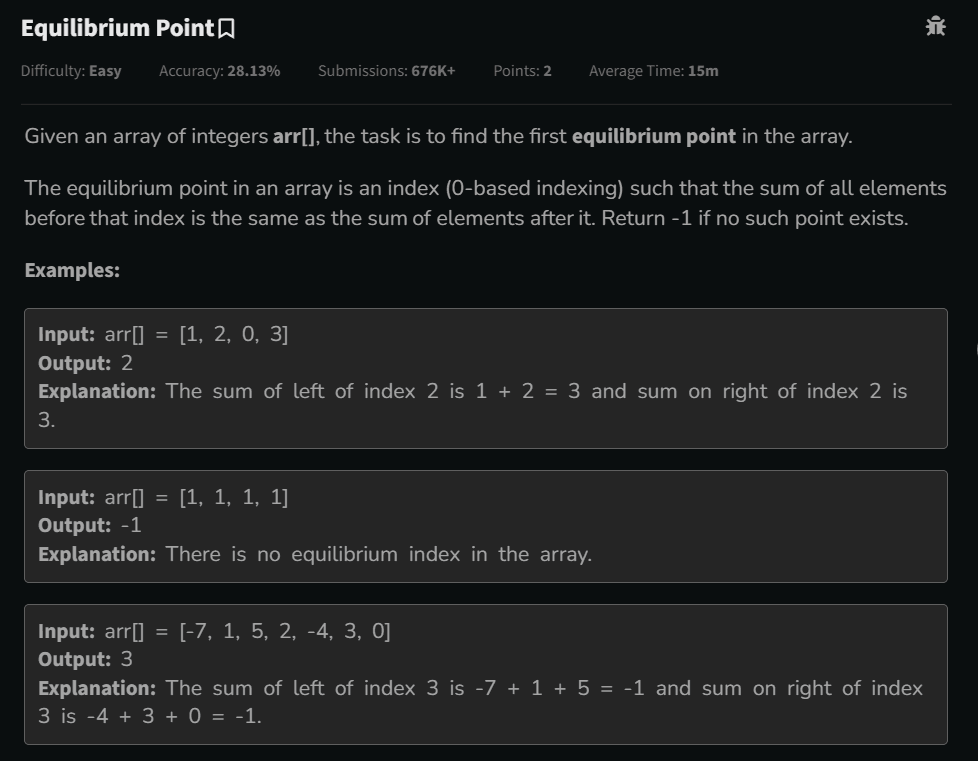
Given an array of integers arr[], the task is to find the first equilibrium point in the array.
The equilibrium point in an array is an index (0-based indexing) such that the sum of all elements before that index is the same as the sum of elements after it. Return -1 if no such point exists.
Examples:
Constraints:
3 <= arr.size() <= 105
-104 <= arr[i] <= 104
Solution:
Solving the Equilibrium Index Problem
The core logic of this problem is finding the Prefix Sum and Suffix Sum. The goal is to identify the specific index where the sum of elements on the left equals the sum of elements on the right.
For beginners, this problem can feel difficult because it isn't immediately obvious how to "balance" the two sides of an array. Understanding these two concepts makes the solution simple:
- Prefix Sum: The cumulative sum of elements from left to right. We store the total sum at each index as we move forward.
- Suffix Sum: The cumulative sum of elements from right to left. We store the total sum at each index as we move backward.
By comparing these two sums, you can easily find the Equilibrium Point where the two halves of the array are equal.