Introduction

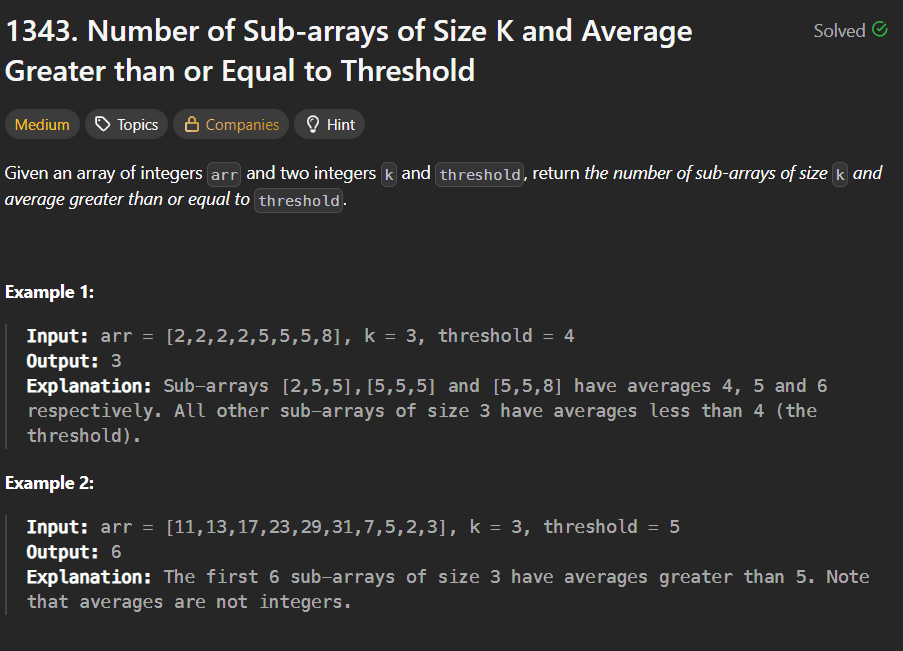
LeetCode 1343: Number of Sub-arrays of Size K and Average Greater than or Equal to Threshold is another excellent problem to practice the sliding window technique.

The goal is not just to compute values but to count how many subarrays satisfy a given condition efficiently.

You are given:

1. An integer array arr
2. An integer k representing subarray size
3. A threshold value

You must return the number of subarrays of size k whose average is greater than or equal to the threshold.

If you'd like to try solving the problem first, you can attempt it here:

👉 Try the problem on LeetCode:

https://leetcode.com/problems/number-of-sub-arrays-of-size-k-and-average-greater-than-or-equal-to-threshold/

Problem Understanding

A direct approach would calculate the average for every subarray of size k. However, recomputing sums repeatedly leads to unnecessary work.

To optimize, we use a sliding window, allowing us to reuse previous computations and move efficiently across the array.

Key Idea: Sliding Window Optimization

Instead of calculating sums repeatedly:

1. Maintain the sum of the current window.
2. Slide the window by:
3. Adding the next element
4. Removing the element leaving the window
5. Check if the average satisfies the threshold.
6. Count valid windows.

This ensures each element is processed only once.

Approach

1. Maintain two pointers to represent the window.
2. Add elements until window size reaches k.
3. Check if average meets the threshold.
4. Move the window forward.
5. Count valid subarrays.

An important optimization: instead of computing average each time, we can compare the sum with threshold * k. However, your current implementation using division also works correctly.

Implementation (Java)

Dry Run Example

Input:

Valid subarrays:

Total valid subarrays = 3

Complexity Analysis

Time Complexity: O(n)

Each element enters and leaves the window once.

Space Complexity: O(1)

Only constant extra variables are used.

Edge Cases Considered

1. Threshold equals zero
2. Minimum array length
3. Large array sizes
4. Non-integer averages
5. All elements smaller than threshold

Sliding Window Pattern Importance

This problem reinforces the sliding window pattern, which appears frequently in:

1. Fixed-size window problems
2. Maximum or minimum subarray problems
3. Counting valid segments
4. String window problems

Mastering this pattern helps solve many interview questions efficiently.

Conclusion

This problem is a strong example of turning a potentially expensive brute-force approach into an efficient linear solution using sliding window.

Once you recognize this pattern, many array and string problems become significantly easier to solve.